|
|||||||||||
Approximate Construction of Regular PolygonsIan Mallett, Brenda Mallett, Russell Mallett, 2006-05-22 Abstract:Some regular polygons with \(n\) sides are classically "constructible" using only a compass and a straightedge, whereas others have been proven by Gauss to be "unconstructable", at least exactly. We develop a practical general procedure for the approximate construction of regular polygons which works well for large \(n\) and which can be adapted for small \(n\). Introduction:Ian, then 14, was interested in finding approximate and practical ways to construct regular polygons that are impossible to construct exactly if using only a compass and straightedge. The geometry computer program "Geometer's Sketchpad" was used to develop a construction for an approximate regular heptagon (for comparison, other procedures for doing this have been described by Dixon: Mathographics. New York: Dover, 1991, reprinted http://mathworld.wolfram.com/Heptagon.html). The algorithm was then extended for the construction of a nonagon (comparing favorably with traditional constructions, as shown by Dixon: http://mathworld.wolfram.com/Nonagon.html). With assistance, the algorithm was generalized to construct polygons for any \(n\). We term this algorithm, and its improvements, the "fraction of a radius" technique. Discussion:
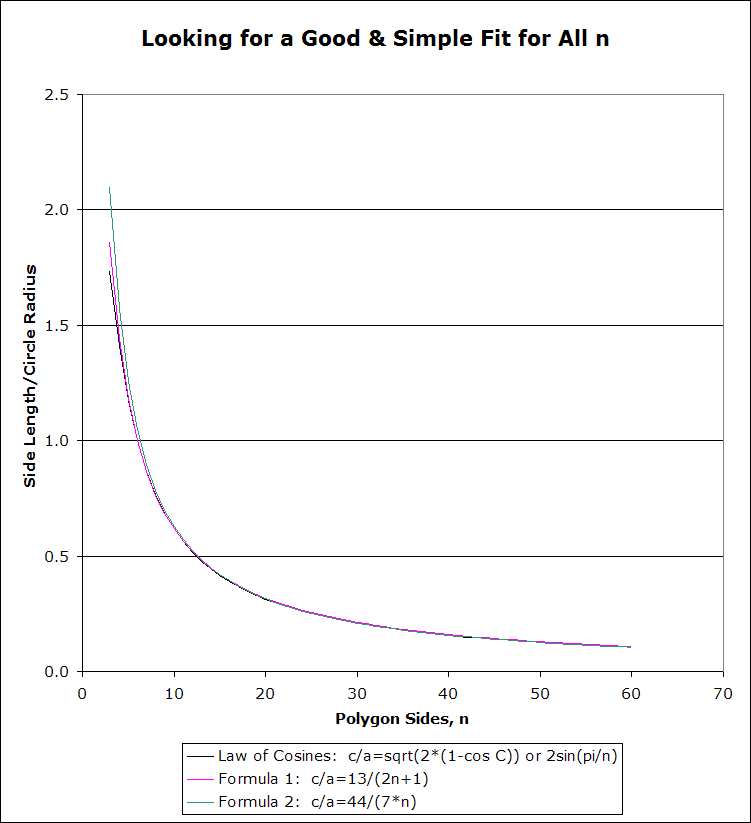
Ian then set out to come up with a method for nonagons. Using the above method of dividing the radius, a nonogon may be constructed by choosing \(\frac{13}{19}\) of the radius. In this case, the error is even less; the central angles are a little over \(0.01^{\circ}\) too large, each. The pattern was generalized for any \(n\) as follows: To approximately construct a regular polygon of \(n\) sides, mark off side lengths around a circle with a fraction \(F\) of its radius equal to:\begin{equation} F = \frac{13}{2 n + 1} \end{equation} Harold Jacobs, author of Geometry: Seeing, Doing, Understanding, suggested we evaluate the algorithm using the Law of Cosines. The Law of Cosines states that \(c^2 = a^2 + b^2 - 2 a b \cos(C)\), where \(a\), \(b\), and \(c\) are the sides of a general triangle and \(C\) is the angle opposite side \(c\). In the case of the fraction of the radius procedure, both \(a\) and \(b\) are the radius of the circle, and \(c\) represents the length of one side of the polygon. \(C\) is the central angle opposite \(c\), and for a regular polygon of \(n\) sides is equal to \(\frac{360^{\circ}}{n}\) (or \(\frac{2 \pi}{n}\)). Since the number of interest for construction by the fraction of the radius procedure is the polygon side length \(c\) divided by the radius of the circle \(a\), one may solve the Law of Cosines for the fraction \(\frac{c}{a} = \sqrt{2 (1 - \cos(C))}\). A quick numeric comparison of this desired \(\frac{c}{a}\) with that given by \(\frac{13}{2 n + 1}\) for increasing \(n\) shows that the approximation is a remarkably good fit for such a simple formula (see Figure 2). Note that Equation 1 works exactly for a hexagon and extremely well for nonagons. The individual central angles constructed become less accurate up to \(n = 23\), although they are still accurate to within a quarter of a degree, then very slowly improve for remaining \(n\); however, the improvement is overcome by the multiplicative effect of increasing \(n\), so that for the polygon as a whole the cumulative error slowly increases with \(n\). Russ, using the trig identity \(1 - \cos(C) = 2 sin^2(C)\) rearranged the Law of Cosines (\(C\) in radians):\[ \frac{c}{a} = 2 \sin\left( \frac{\pi}{n} \right) \]For small central angle \(C\) (i.e., large \(n\)), the first-order Taylor approximation \(\sin(\theta) \approx \theta\) holds, giving:\[ \sin\left( \frac{\pi}{n} \right) \approx \frac{\pi}{n}\\ \frac{c}{a} \approx \frac{2 \pi}{n} \]Equating \(\frac{13}{2 n + 1}\) to this and solving for \(\pi\), one obtains:\[ \pi \approx \lim_{n \rightarrow \infty} \frac{n}{2} \frac{13}{2 n + 1} = \frac{13}{4} \] Using a better fractional approximation of \(\pi \approx \frac{22}{7}\), one obtains an improved "fraction of the radius" formula:\begin{equation} \frac{c}{a} = \frac{44}{7 n} \end{equation} One may continue refining the algorithm by using another approximation for \(\pi\), such as \(\frac{355}{113}\), but the physical compass and straightedge procedure would quickly become unrealistic, with merely an asymptotic gain in accuracy. The improvement from \(\frac{13}{4}\) to \(\frac{22}{7}\) is justified, however; Equation 2 is much better than Equation 1 for \(n > 14\) (see Figure 3). For example, for \(n = 25\), Equation 1 results in central angles more than \(0.24^{\circ}\) too large, for a cumulative error over the \(25\) angles of over \(6^{\circ}\), while Equation 2 results in central angles just over \(0.04^{\circ}\) too large, for a cumulative error of only a litle over \(1^{\circ}\). In contrast to Equation 1, Equation 2 only improves with increasing \(n\), for both individual central angles and for polygons as a whole.
After using common exact constructions for \(n = 3, 4, 5,\) and \(6\), one might reasonably continue with the Equation 1 approximation for \(n = 7, 9, 11, 13,\) and \(14\), with Equation 2 for higher \(n\) where inexact constructions are impossible. However, Russ suggests that, for a highly accurate polygon of small \(n\), one could merely construct a polygon with a convenient integer multiple of \(n\) sides, but only connect a corresponding fraction of the vertices (for example, construct a regular \(21\)-gon, and connect every third vertex to form a heptagon. We call this process "superconstruction/division". It is worth noting that regular polygons of any degree may be constructed to arbitrary precision using this method. Conclusion:We have presented a successful general rule for the approximate construction of regular polygons. The rule may be extended in simple manners—either by better approximating \(\pi\), or by superconstruction/division. Using these extensions, this simple and straightforward method can be used to construct polygons of any \(n\) to any precision desired using only the classic geometric instruments.
|
|||||||||||
| |||||||||||
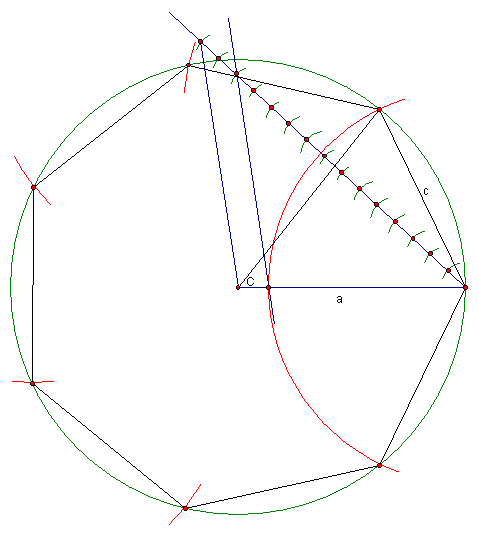Figure 1: Approximate construction of a regular heptagon via the "fraction of the radius" technique.
