Light and Color: Introduction to Radiometry, Photometry, and Colorimetry
Introduction
Radiometry, Photometry, and Colorimetry are in some sense pre-requisites to rendering, but they are not rendering per-se.
Put simply, Radiometry (literally: "light measurement") is the science of how light works—the actual physical photons moving around the world. When we are writing a renderer, we are simulating this actual
Conversely, Colorimetry is the perceptual study of how light appears to the human visual system. There's quite a bit of science in it, too. Colorimetry depends upon the light simulated from Radiometry. It is the final step in rendering, not the tool to render per-se.
Photometry blends the two, doing light measurement weighted by human luminance sensitivity. Photometry is mainly useful for people who are not doing graphics, but it is frequently confused with Radiometry, and comes with its own units that we do need to deal with when creating rendered images for display.
Radiometry and Radiometric Units
Radiometry describes how actual light propagates. In graphics, it is the tool that lets us figure out how much light from the light source(s) in the scene is absorbed by sensor(s) of the scene (think: cameras or eyes). Taking pathtracing as an example, we randomly select paths from the sensor(s) to light source(s). Estimating the light propagating along the path, and averaging the results of many such estimates in the careful formalism of a Monte Carlo method, gives us the total light hitting the pixel.
Understanding Radiometry, separate from a rendering technique, is mostly a question of understanding what the units are. We'll define all units below, but to give a flavor: the light from the light sources is usually measured in
Radiometry works in physical units, based on SI[1]. Unfortunately, the units have a rich history and their names are sometimes used for different things in other fields (mainly in Physics). The usage here will be correct for graphics.
It's important to note that there are also
In graphics, we really 'should' be talking about spectral units, since these are the units in which you actually write your renderer. However, in practice, this is an extra dimension and it's obvious from context anyway which one we're talking about, so most of the time everyone just drops the distinction and describes their renderer in non-spectral units.
Without further ado, everyone who does physically based rendering thoroughly knows and understands the following radiometric quantities:
Radiant Energy
Radiant Flux
You usually only see radiant flux by itself at the beginning or end of rendering (the power of the lights or the power accumulated on the sensor, respectively). However, throughout the rendering process, other quantities are used, all based on radiant flux as a primitive.
The units of radiant flux are Watts (\(\unitsW\)), and the ubiquitous symbol is \(\Phi\).
Radiant Flux Density: Irradiance, Radiant Exitance, Radiosity
The most common place you see irradiance nowadays is in the rendering equation. The incoming radiance (see below) gets multiplied by the geometry term, which converts to differential area on the surface, while we're integrating over the (hemi)sphere, which cancels the differential solid angle—together, the result is irradiance. (Note that the BRDF/BSDF is the ratio of outgoing radiance to incoming radiance, so multiplying by it gives us radiance for the final output, propagating the cycle to the next bounce.)
Radiant Intensity
Radiance, Importance
Radiance is the common intermediary when doing rendering because, amazingly, it is invariant along straight rays (that is, it doesn't change with distance). This makes some sense if you remember the intuitive definition as brightness: a lightbulb doesn't look brighter per-se when you get closer to it. You certainly receive more energy because it fills more of your field of view, but any individual point on it doesn't look brighter. This property of distance invariance makes radiance extremely convenient for rendering.
The units for both radiance and importance are Watts per steradian per projected area (\(\unitsL\)). Importance doesn't have a standard symbol, but the symbol for radiance is[3] \(L\):
\[ L ~~=~~ \frac{ d^2 \Phi }{ d\omega ~dA \cos(\theta) } ~~=~~ \frac{ d^2 \Phi }{ d\omega ~dA^\perp } \]Using \(dA^\perp\) is probably the better notation: it stresses that the differential area is considered to be perpendicular to the direction of the ray. However, the cosine is nice for showing how it can be canceled in the rendering equation.
Photometry
Photometry is like Radiometry, except that it describes perceptual brightness. While Radiometry concerns the physical power of light, Photometry says how it looks. In Radiometry, we might consider a single photon, which has a spectral radiant energy: the joules carried by that particular photon. What Photometry tells us is how much this matters to perception.
SI defines that light at \(540~\unitsTHz\) will produce exactly \(K_{\text{cd}}:=683~\units{\unitlm/\unitW}\) of luminous flux.
What's luminous flux? Basically, it's radiant flux (\(\unitsW\)), but centered around how bright it looks to a human, giving a new unit, the lumen (\(\units{\unitlm}\)). Just like there are radiometric units built around watts, there are photometric units built around the lumen. For example, radiant intensity (radiometric, \(\units{\unitW/\unitsr}\)) corresponds to luminous intensity (photometric, candela \(\units{\unitcd}\)). (For all the correspondences, see table in next section.)
Of course, photons come at many different frequencies, and perceived brightness varies with respect to that. E.g., if the photon is red or violet, it won't look as bright as if it were green. The way we handle this is by a dimensionless weighting function, the luminous efficiency function \(V(\lambda)\), which says how bright a wavelength \(\lambda\) looks to the human eye, expressed relative to the peak value, \(V(555~\unitsnm) = 1\). In practice, \(V(\lambda)\) is tabulated data that you can just download.
The \(540~\unitsTHz\) light above was chosen to have a wavelength close to \(555~\unitsnm\). Still, it's a bit off (\(\lambda \approx 555.016~\unitsnm\)), meaning that light at exactly \(540~\unitsTHz\) is actually a smidge dimmer than the peak[4]. Specifically, \(540~\unitsTHz\) (\(\approx 555.016~\unitsnm\)) light produces \(K_{\text{cd}}:=683~\units{\unitlm/\unitW}\) of luminous flux, while \(555~\unitsnm\) light produces \(K_{\text{cd},\lambda}=683.002~\units{\unitlm/\unitW}\) of luminous flux.
For a combination of different wavelengths, we integrate the spectrum with the weighting function. Formally, for a given spectral power distribution, computed from Radiometry, of radiant intensity \(I(\lambda)\), we integrate, weighting by \(V(\lambda)\), to get the corresponding photometric quantity, luminous intensity \(I_v\), of the whole spectrum:
\[ I_v = K_{\text{cd},\lambda}\int_0^\infty I(\lambda) \, V(\lambda) \, d\lambda \] \[ K_{\text{cd},\lambda} = 683.002~\units{\unitlm/\unitW} \]Note that this equation works for any corresponding units. Although it is defined for radiant intensity and luminous intensity, it will also work for radiance and luminance, for radiant flux and lumens, and so on.
Photometric units are not yet commonly used in computer graphics because the non-physical-ness seems repellant to accurate simulation of light. However, as we shall see, we can't get around invoking at least a little bit of Photometry for image display (we will address this below). Outside of graphics, Photometry is very popular in fields such as architecture and consumer lighting, where it allows for rough estimations of indoor illumination.
Radiometric and Photometric Units Summary
| Radiometry | Photometry | |||
|---|---|---|---|---|
| Quantity | SI Unit | Symbolic | Quantity | SI Unit |
| Radiant Energy | \(\unitsJ\) | \(Q\), \(J\) | \(\units{\unitlm\cdot\unitsec} = \units{\unitcd\cdot\unitsr\cdot\unitsec}\) ( | |
| Radiant Flux | \(\unitsW\) | \(\Phi\) | \(\units{\unitlm} = \units{\unitcd\cdot\unitsr}\) ( | |
| Irradiance | \(\unitsE\) | \(E=d\Phi_{\text{in}}/dA\) | \(\units{\unitlx} = \units{\unitlm/\unitm^2} = \units{\unitcd\cdot\unitsr/\unitm^2}\) ( | |
| Radiant Exitance | \(\unitsE\) | \(M=d\Phi_{\text{out}}/dA\) | \(\units{\unitlm/\unitm^2}\) (note[6]) | |
| \(\units{\unitJ/\unitm^2}\) | \(\units{\unitlx\cdot\unitsec}\) | |||
| Radiant Intensity | \(\units{\unitW/\unitsr}\) | \(I=d\Phi/d\omega\) | \(\units{\unitcd} = \units{\unitlm/\unitsr}\) ( | |
| Radiance | \(\unitsL\) | \(L=d^2\Phi/(d\omega\cdot dA^\perp)\) | \(\units{\unitcd/\unitm^2} = \units{\unitlm/(\unitsr\cdot\unitm^2)}\) ( | |
Colorimetry
We have an incoming spectrum of light calculated from Radiometry. If the virtual world were real, that spectrum of light would be real. It would be entering our eyes and giving an impression of color and brightness. The goal of Colorimetry is simply to set pixels on the screen that will induce a similar impression when the viewer looks at it.
A key reference for the details of colorimetric calculations is CIE 015 (older 3rd Ed. here).

Figure 0
: Approximate standard "long" ("L") / "medium" ("M") / "short" ("S") cone sensitivities as functions of frequency, normalized to \(1.0\). (Image Source)Cone Response
Most people have three different kinds of color receptors in their eyes (see response functions in Figure 0), which are sensitive to broad, different, ranges of electromagnetic radiation. For example, if \(450~\unitsnm\) light enters your eye, the 'short' cones are stimulated strongly. If \(600~\unitsnm\) light enters your eye, the 'long' cones are stimulated strongly, while the 'medium' cones are stimulated only somewhat. In general, each input produces a response for each of the three types of cone.
Usually, of course, an entire spectral power distribution, comprising many different frequencies at different strengths, enters your eye all at once. The cones' response is just the integral of their response over wavelength, and you still only get one response for each type of cone. At the end of the day, it is only these three scalar values that go to your brain to represent that whole infinite-dimensional space of possibility.
Mathematically, for a given spectral power distribution computed from Radiometry, which describes the relative strength[7] of radiation with respect to wavelength (call it \(s(\lambda)\)), we integrate with the 'cone fundamentals' functions \(\bar{l}(\lambda)\), \(\bar{m}(\lambda)\), and \(\bar{s}(\lambda)\), which again are simply tabulated data that you can just download[8]:
\[ L = \int_0^\infty s(\lambda) \, \bar{l}(\lambda) \, d\lambda,\hspace{1cm} M = \int_0^\infty s(\lambda) \, \bar{m}(\lambda) \, d\lambda,\hspace{1cm} S = \int_0^\infty s(\lambda) \, \bar{s}(\lambda) \, d\lambda \]The three resulting numbers \(\vecinline{L,M,S}\) make a 3D space, the LMS Color Space. Every possible spectrum boils down to a point in this space. This triple uniquely and completely describes the appearance of the incoming spectral power distribution to the human visual system.
Note that two completely different spectral power distributions can just happen to produce the same integrals, and so the same three responses, and so the same appearance. In fact, for a given triple, an infinite number of different spectral power distributions can produce it. This is correct; it's a phenomenon known as '
The CIE Standard Observer
Researchers soon developed the CIE RGB color-space, a linear transform of the LMS color-space that had primaries that could be clearly called red, green, and blue. Unfortunately, the CIE RGB color-space had issues—in particular, some colors were outside its gamut, resulting in negative values, which was inconvenient for the manual math of the 1920s/30s.
Thus, researchers came up with a different transformation, producing the CIE 1931 XYZ Color Space. Although the primaries are not red/green/blue, the Y primary semantically represents relative 'brightness', and importantly all colors and the matching functions are nonnegative. Several other convenient properties were enforced too.
The XYZ color-space works very similarly to the LMS color-space. The three functions are \(\bar{x}(\lambda)\), \(\bar{y}(\lambda)\), and \(\bar{z}(\lambda)\) (together called the
The result of this inner product operation is again a vector of three nonnegative numbers \(\vecinline{X,Y,Z}\). In this case, the tuple is called the CIE
Units and Luminance Doublethink
The CIE XYZ space has no units. The implications of this are confusing and subtle, and mostly concern \(Y\).
Although \(Y\) 'represents' luminance, it is only proportional to luminance (\(\unitsnit\)), and has no units on its own. (\(X\) and \(Z\) 'represent' hue, and so perhaps it is intuitive that they don't have units either.) The tristimulus triples are only used in comparison to other spectra integrated into XYZ. Actually, we usually only determine what the numerical values mean during a later conversion to another color-space. (We will define more precisely how this is done below, for the primary example, sRGB.)
\(Y\) 'represents' luminance in the sense that the luminous efficiency function \(V(\lambda)\) discussed above is actually the 'same' function semantically[10] as \(\bar{y}(\lambda)\). The scaling becomes apparent if we compare the above definitions of luminous intensity \(I_v\) versus the \(Y\)-coordinate of CIE XYZ:
\begin{alignat*}{2} I_v &= K_{\text{cd},\lambda}&\int_0^\infty I(\lambda) \, V(\lambda) \, d\lambda \\[1em] Y &= &\int_0^\infty s(\lambda) \, \bar{y}(\lambda) \, d\lambda \end{alignat*}The luminous intensity definition works for other radiometric quantities as well, so in particular \(I(\lambda)\) in radiance (\(\unitsL\)) gives us \(I_v\) in luminance (\(\unitsnit\)). If we wanted \(Y\) to be in \(\unitsnit\) too, we can infer that it is too small by a factor of \(K_{\text{cd},\lambda} = 683.002~\units{\unitlm/\unitW}\).
That is, when \(s(\lambda)\) in radiance (\(\unitsL\)), the units of \(Y\) are numerically \(1/683.002 \approx 0.00146412~\units{\unitnit/\unitunit}\), up to the approximation[10] \(s(\lambda)\,\bar{y}(\lambda) \approx s(\lambda)\,V(\lambda)\). Despite the fact that significant upgrades are known, the 1924 \(V(\lambda)\) is apparently still used as the basis of luminance and the CIE 1931 space (and its \(\bar{y}(\lambda)\)) is still critical to modern colorimetry.
Again though, the CIE XYZ space is not considered to have units. The solution, apparently, is to not think of \(V(\lambda)\) and \(\bar{y}(\lambda)\) the same way, despite the fact that they are the same function (or very similar, numerically). I think the difference arose due to the history of how these concepts were discovered / invented, but the difference itself has confused countless graphics programmers (including myself) over the years—if not pretty much everyone[11].
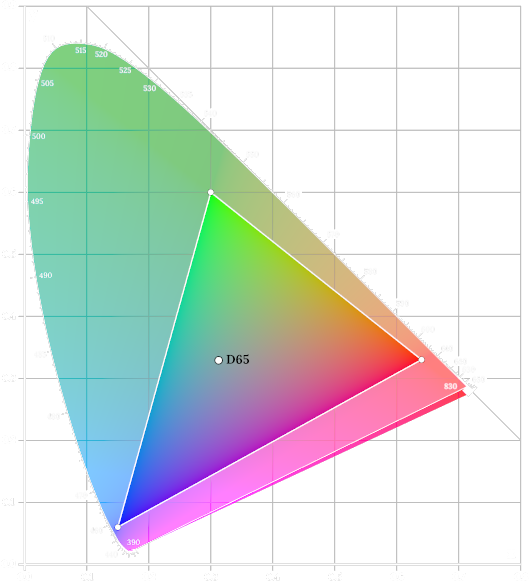
Figure 1
: The CIE xy diagram and the triangular "gamut" within it that can be displayed by the sRGB color standard. Note: the gamut is approximate; the chart is based on 2006 data, but sRGB's gamut coordinates are referred to 1931 data; see[12]. (Image by me.)Chromaticity
You can normalize the \(\vecinline{X,Y,Z}\) tristimulus triple:
\[ \begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix}X\\Y\\Z\end{bmatrix} \bigg/ (X+Y+Z) \]The combination of \(x\), \(y\), and \(Y\) forms the
The \(\vecinline{x,y}\) coordinates are the space of color (color is two-dimensional), and the third coordinate \(Y\) is relative brightness, as above. The perimeter of the horseshoe-shaped region corresponds to spectra with only one wavelength—i.e. the rainbow. The rainbow is the 1D boundary of the 2D region of color, and therefore (fun fact) the rainbow contains exactly 0% of all color by area!
Any point in the xy chart is called a '
Displays and Colors
At this point, we have converted our radiometric spectrum into the \(\vecinline{X,Y,Z}\) tristimulus triple representing, indirectly, the actual responses of cone cells within the human eye. Now, we need to transform it so that we can induce those responses, or at least some semblance of those responses, by setting pixels to certain colors.
While the idea is straightforward, the reality is that there are many different ways to do this because modern displays (though amazing) simply are unable to reproduce the richness of the real world. (Enter
Adding to the complexity: because everything is terrible, screens will often do their own thing instead of producing repeatable colors. For example, a typical phone screen will brighten and darken, and will oversaturate colors on-purpose to make them look more "vibrant". While this is arguably more appealing, it is usually uncontrollable, making correct reasoning about formal Colorimetry somewhere between challenging and impossible.
sRGB
Essentially every color screen today supports a color standard called sRGB[14]. The best way I've found to think about sRGB is that it encompasses both a color-space and an encoding—that is, a description of the colorimetric properties of the system, and a way of representing it[15].
While sRGB is an old standard and new screens can do much better, unfortunately, by this point sRGB is so dominant that better color-spaces are finding it hard to gain programmatic traction, with any exposition to software APIs being clunky and platform-specific—so sRGB conversion, while basic, is still the primary way we get pixels on the screen today. The attractiveness of sRGB is that you can blast three bytes per pixel onto nearly any screen in existence and get something reasonable out. There is currently no equivalent for more modern color-spaces, superior though they may be in theory.
In short, the sRGB standard is the sine qua non of display technology and RGB color-spaces (for better or for worse), so we should at least talk about the basic way to convert \(\vecinline{X,Y,Z}\) tristimulus values into sRGB bytes.
The Colorimetry of sRGB
The sRGB color-space is defined by three '
The primaries form a triangle in chromaticity space, which is sRGB's '
The '
The XYZ coordinates of D65 under the 1931 standard observer are approximately \(\vecinline{1.00437,1.05671,1.15057}\times10^{-5}\). The brightness if we interpreted that as luminance (multiply \(Y\) by \(K_{\text{cd},\lambda}\)) would therefore be about \(0.00721734~\unitsnit\). The scaling factor to bring that back to \(80~\unitsnit\) would be about \(11084.4\). So, this factor times D65 is the white point of sRGB. The XYZ coordinates of this scaled spectrum are roughly \(\vecinline{0.111329,0.117130,0.127534}\).
sRGB Conversion: XYZ to ℓRGB
The three primaries with the white point are used to calculate a matrix[19] \(M\), whose inverse \(M^{-1}\) intuitively transforms \(\vecinline{X,Y,Z}\) into linear \(\vecinline{R,G,B}\) (which I call "ℓRGB" for clarity—a usage that seems to be gaining traction). It is 'linear' RGB to contrast with the final sRGB, which has a nonlinear gamma encoding (next section).
The actual transformation is widely seen online in a form that is simplified to the point of error (or at least contextual uselessness). The transformation matrix does indeed transform from ℓRGB to XYZ, and the space is re-scaled so that the white point transforms to \(Y_W=1\). That is, RGB white has XYZ coordinate \(Y=1\). True, this seems like the most natural way to convert the spaces in isolation, but the detail of \(Y_W=1\) is commonly overlooked, nearly as often omitted from reference material, ends up adding computational overhead that could have been avoided by appropriate units, and has nontrivial implications about how scene luminance must be handled that are never explained.
The key point is that you take your scene's spectral radiance, compute the XYZ values from that, and then these XYZ values must all be normalized by the white point. I.e., after you calculate the XYZ values, you have to divide them by \(Y_W \approx 0.117130\), the brightness of the white point. Wherefore, the actual transformation:
\[ \text{ℓRGB} = \begin{bmatrix}R\\G\\B\end{bmatrix} ~~=~~ \left( M^{-1} \right) \left( \frac{1}{Y_W} \begin{bmatrix}X\\Y\\Z\end{bmatrix} \right) \]Where:
\[ M^{-1} ~~=~~ \begin{bmatrix} \phantom{-}3.2406 & - 1.5372 & - 0.4986\\ - 0.9689 & \phantom{-}1.8758 & \phantom{-}0.0415\\ \phantom{-}0.0557 & - 0.2040 & \phantom{-}1.0570 \end{bmatrix} \]That matrix is the 'official' version from the sRGB specification; a more-precise matrix can be computed using the definitions and linked algorithm above, if you prefer that. (This is indeed what I myself do, though I'm not sure I recommend it in general, as the results will be (very slightly) different from the standard. They will also be more colorimetrically accurate though, so . . . 🤷)
This formalism implements a 'portal' effect. You want your image of your rendered world to be seen by the viewer as if they were looking at it physically. This basically means that the real-world radiance emitted from the screen is (a metamer for) the radiance you are simulating in the virtual world.
The transformation does this. Suppose you have a gray virtual object emitting at \(16~\unitsnit\), which is \(20\unitspercent\) the brightness of white. This will produce an XYZ value of roughly \(\vecinline{0.0222657,0.0234260,0.0255069}\). We now normalize it by the white point by dividing by \(Y_W \approx 0.117130\), to get roughly \(\vecinline{0.190094,0.200000,0.217766}\). We multiply by the matrix to get RGB \(\vecinline{0.2,0.2,0.2}\). This causes the screen to produce something like white, but at \(20\unitspercent\) the brightness (\(16~\unitsnit\) instead of \(80~\unitsnit\)). This is what we wanted.
Now, \(80~\unitsnit\) is fairly dim and data can easily exceed this (e.g. a picture of the Sun would be \(1.6\times 10^9~\unitsnit\)). The sRGB standard says such values should be clipped[16], or we can add an additional factor of dimming, which we can think of as an exposure value. There's also tonemapping, as above. None of this is colorimetrically sound, but human observers get the point regardless.
sRGB Conversion: ℓRGB to sRGB (Gamma Encoding)
The final step of sRGB conversion is to convert the ℓRGB triple of floating-point values into the sRGB triple of bytes. There's obviously a quantization, but there's also a nonlinear transformation called the
The gamma transform is pretty simple, though much nonsense has been written about it too. Basically, when we convert from a float to a byte, we lose a lot of precision. Each byte has only has 256 possible values, so we need to be careful about how we allocate that coding space. The human visual system is nonlinear, so it makes sense for the brightnesses signified by these 256 values to also be distributed nonlinearly. Equivalently, the screen should have a nonlinear response to input[20]. The gamma transform is this nonlinearity.
In sum: we apply the inverse gamma transform to the floating-point data, quantize to bytes, and send it to the screen. The display hardware then applies the forward gamma transform, displaying nonlinear brightnesses. These nonlinear brightnesses are interpreted by the nonlinear human visual system in a way where the quantization inaccuracy is spread over the range of brightnesses fairly evenly.
The particular transformation the sRGB standard uses is a combination of a power law and a linear bias[21]. The specifics aren't very interesting; see the link for particulars. But, to save you (and me!) the trouble, here are implementations in Python and C++ that do the conversions:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class lRGB:
def __init__( self, r:float,g:float,b:float ):
self.r=r; self.g=g; self.b=b
class sRGB:
def __init__( self, r:int ,g:int ,b:int ):
self.r=r; self.g=g; self.b=b
# gamma + quantization
def srgb_gamma_encode( val:float ):
assert val >= 0.0
if val >= 1.0 : return 255
if val <= 0.0031308: val = 12.92 * val
else : val = 1.055*pow(val,1.0/2.4) - 0.055
return int(round( 255.0 * val ))
# unpack and inverse gamma
def srgb_gamma_decode( val:int ):
tmp = float(val) / 255.0
if tmp <= 0.04045: return tmp / 12.92
else: return pow( (tmp+0.055)/1.055, 2.4 )
# conversions between sRGB and lRGB
def lrgb_to_srgb( lrgb:lRGB ):
r = srgb_gamma_encode(lrgb.r)
g = srgb_gamma_encode(lrgb.g)
b = srgb_gamma_encode(lrgb.b)
return sRGB( r, g, b )
def srgb_to_lrgb( srgb:sRGB ):
r = srgb_gamma_decode(srgb.r)
g = srgb_gamma_decode(srgb.g)
b = srgb_gamma_decode(srgb.b)
return lRGB( r, g, b )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <cassert>
#include <cmath>
#include <cstdint>
struct lRGB final { float r, g, b; };
struct sRGB final { uint8_t r, g, b; };
// gamma + quantization
[[nodiscard]] constexpr uint8_t srgb_gamma_encode( float val ) noexcept
{
assert( val >= 0.0f ); // Note catches NaN too.
#if 0
if ( val >= 1.0f ) return 255;
val = val<0.0031308f ? val*12.92f : 1.055f*std::pow(val,1.0f/2.4f)-0.055f;
return (uint8_t)std::round( 255.0f * val );
#else
if ( val >= 1.0f ) [[unlikely]] return 255;
else if ( val <= 0.0031308f ) [[unlikely]] val *= 255.0f*12.92f;
else [[likely]]
{
val = std::pow( val, 1.0f/2.4f );
val = std::fma( 255.0f*1.055f,val, 255.0f*-0.055f );
}
return (uint8_t)std::round(val);
#endif
}
// unpack and inverse gamma
[[nodiscard]] constexpr float srgb_gamma_decode( uint8_t val ) noexcept
{
#if 0
float tmp = (float)val / 255.0f;
tmp = tmp<0.04045f ? tmp/12.92f : std::pow((tmp+0.055f)/1.055f,2.4f);
return tmp;
#else
float tmp = (float)val;
if ( val <= 10 ) [[unlikely]] // `tmp <= 0.04045f*255.0f`
{
tmp *= (float)( 1.0 / (12.92*255.0) );
}
else [[likely]]
{
tmp = std::fma( (float)(1.0/(1.055*255.0)),tmp, (float)(0.055/1.055) );
tmp = std::pow( tmp, 2.4f );
}
return tmp;
#endif
}
// conversions between sRGB and lRGB
[[nodiscard]] constexpr sRGB lrgb_to_srgb( lRGB const& lrgb ) noexcept
{
uint8_t r = srgb_gamma_encode(lrgb.r);
uint8_t g = srgb_gamma_encode(lrgb.g);
uint8_t b = srgb_gamma_encode(lrgb.b);
return { .r=r, .g=g, .b=b };
}
[[nodiscard]] constexpr lRGB srgb_to_lrgb( sRGB const& srgb ) noexcept
{
float r = srgb_gamma_decode(srgb.r);
float g = srgb_gamma_decode(srgb.g);
float b = srgb_gamma_decode(srgb.b);
return { .r=r, .g=g, .b=b };
}
Note that the C++ version includes a simple implementation and an optimized implementation. Modern architectures have FMA instructions (compile with "-mfma"), so it makes sense to specify that we do the scale and bias with FMA—the compiler probably won't give you this automatically even with high optimizations[22]. We also, of course, replace the divisions by reciprocal multiplication, and combine some constants. Admittedly, these basic optimizations are somewhat futile; the slowest part by far is the power function—which is actually quite difficult to optimize without losing an unacceptable amount of precision. I'm working on a version that's much faster, but as yet it's more complicated and still only approximate.
Here's some test code to demo gamma encoding / decoding:
